Finding the Roots of a Quadratic Equation is a fundamental problem in algebra and programming. In C programming, solving this problem can be approached in several ways. This article provides a detailed guide on three methods to write a C Program to Find Roots of a Quadratic Equation: the quadratic formula, factoring, and completing the square. We explain each method with code examples, explanations, and expected outputs to help you understand and implement these techniques effectively.
Write a C Program to find Roots of a Quadratic Equation
What is Quadratic Equation?
A quadratic equation is generally represented as:
ax2+bx+c=0
where a, b, and c are coefficients, and x represents the variable. The solutions or roots of this equation can be real or complex, depending on the discriminant b2−4ac.
Method 1) C program to find Roots of a Quadratic Equation using the Quadratic formula
The quadratic formula is a popular method for finding the roots of a quadratic equation. We derive it from the process of completing the square and express it as:
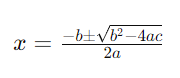
This formula works for all quadratic equations, including those with complex roots.
Code Example
#include <stdio.h>
#include <math.h>
void findRootsUsingFormula(float a, float b, float c) {
float discriminant = b * b - 4 * a * c;
float root1, root2;
if (discriminant > 0) {
// Two distinct real roots
root1 = (-b + sqrt(discriminant)) / (2 * a);
root2 = (-b - sqrt(discriminant)) / (2 * a);
printf("Roots are real and different.\n");
printf("Root 1 = %.2f\n", root1);
printf("Root 2 = %.2f\n", root2);
} else if (discriminant == 0) {
// One real root (repeated)
root1 = root2 = -b / (2 * a);
printf("Roots are real and the same.\n");
printf("Root 1 = Root 2 = %.2f\n", root1);
} else {
// Complex roots
float realPart = -b / (2 * a);
float imaginaryPart = sqrt(-discriminant) / (2 * a);
printf("Roots are complex and different.\n");
printf("Root 1 = %.2f + %.2fi\n", realPart, imaginaryPart);
printf("Root 2 = %.2f - %.2fi\n", realPart, imaginaryPart);
}
}
int main() {
float a, b, c;
printf("Enter coefficients a, b, and c: ");
scanf("%f %f %f", &a, &b, &c);
findRootsUsingFormula(a, b, c);
return 0;
}Explanation of the Code
- Calculate the Discriminant: The discriminant (b2−4ac) determines the nature of the roots.
- Real and Different Roots: When the discriminant is positive, the equation has two distinct real roots.
- Real and Same Roots: When the discriminant is zero, there is exactly one real root that repeats.
- Complex Roots: A negative discriminant indicates complex roots, which are conjugates of each other.
Output
Enter coefficients a, b, and c: 1 -3 2 Roots are real and different. Root 1 = 2.00 Root 2 = 1.00
Method 2) C program to find Roots of a Quadratic Equation using Factoring
Factoring involves expressing the quadratic equation in the form (px+q)(rx+s)=0. This method works well when you can easily factor the quadratic equation into simpler binomials.
Code Example
#include <stdio.h>
void findRootsByFactoring(float a, float b, float c) {
float root1, root2;
int found = 0;
// Simple brute-force approach for factoring
for (int i = -100; i <= 100; i++) {
for (int j = -100; j <= 100; j++) {
if (i * j == a * c && (i + j) == b) {
root1 = -((float)i) / a;
root2 = -((float)j) / a;
found = 1;
break;
}
}
if (found) break;
}
if (found) {
printf("Roots are real and factored.\n");
printf("Root 1 = %.2f\n", root1);
printf("Root 2 = %.2f\n", root2);
} else {
printf("The equation cannot be factored into real numbers easily.\n");
}
}
int main() {
float a, b, c;
printf("Enter coefficients a, b, and c: ");
scanf("%f %f %f", &a, &b, &c);
findRootsByFactoring(a, b, c);
return 0;
}Explanation of the Code
- Brute-Force Search: This method checks possible integer pairs to find factors that satisfy the quadratic equation.
- Factors and Roots: When we find suitable factors, we use them to determine the roots.
Output
Enter coefficients a, b, and c: 1 -5 6 Roots are real and factored. Root 1 = 2.00 Root 2 = 3.00
Method 3) C Program to find Roots of a Quadratic Equation using Completing the Square
Completing the square transforms the quadratic equation into a perfect square trinomial. This approach simplifies solving for xxx by rewriting the equation as:
a(x−h)2=k
Code Example
#include <stdio.h>
#include <math.h>
void findRootsByCompletingSquare(float a, float b, float c) {
float h, k;
h = -b / (2 * a);
k = (4 * a * c - b * b) / (4 * a);
printf("The equation can be written as: (x + %.2f)^2 = %.2f\n", h, -k);
if (k > 0) {
printf("Roots are complex and different.\n");
printf("Root 1 = %.2f + %.2fi\n", h, sqrt(-k));
printf("Root 2 = %.2f - %.2fi\n", h, sqrt(-k));
} else if (k == 0) {
printf("Roots are real and the same.\n");
printf("Root 1 = Root 2 = %.2f\n", h);
} else {
printf("Roots are real and different.\n");
printf("Root 1 = %.2f\n", h + sqrt(-k));
printf("Root 2 = %.2f\n", h - sqrt(-k));
}
}
int main() {
float a, b, c;
printf("Enter coefficients a, b, and c: ");
scanf("%f %f %f", &a, &b, &c);
findRootsByCompletingSquare(a, b, c);
return 0;
}Explanation of the code
- Transform the Equation: Rewrite the equation to isolate (x−h)2.
- Solve for Roots: Depending on the value of k, determine the nature of the roots.
Output
Enter coefficients a, b, and c: 1 -4 4 The equation can be written as: (x - 2.00)^2 = 0.00 Roots are real and the same. Root 1 = Root 2 = 2.00
Understanding and implementing different methods to write a C program to find the roots of a quadratic equation is essential for solving various mathematical problems. The quadratic formula is universally applicable, factoring is useful for simple cases, and completing the square provides a methodical approach. By mastering these techniques, you can effectively solve quadratic equations and enhance your programming skills in C.