Finding the Least Common Multiple (LCM) of two numbers is a fundamental concept in mathematics, frequently used in programming tasks. In C programming, calculating the LCM is a common exercise that enhances understanding of loops, functions, and recursion. This article will walk you through three detailed methods to find the LCM of two numbers in C, complete with code examples, explanations, and outputs.

Write a C Program to Find LCM of Two Numbers

What is LCM?

The Least Common Multiple (LCM) of two numbers is the smallest positive integer that is divisible by both numbers. For example, the LCM of 4 and 5 is 20 because 20 is the smallest number divisible by both 4 and 5.

Method 1) C Program to Find LCM of Two Numbers using GCD

The most efficient way to find the LCM is by using the Greatest Common Divisor (GCD). The relationship between LCM and GCD is given by:

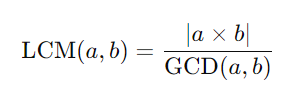
Code Example

#include <stdio.h>

// Function to calculate GCD using Euclidean algorithm
int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}

// Function to calculate LCM using GCD
int lcm(int a, int b) {
    return (a * b) / gcd(a, b);
}

int main() {
    int num1, num2;
    printf("Enter two integers: ");
    scanf("%d %d", &num1, &num2);
    
    printf("LCM of %d and %d is %d\n", num1, num2, lcm(num1, num2));
    return 0;
}

Explanation of the Code

• GCD Calculation: The gcd function computes the Greatest Common Divisor using the Euclidean algorithm, which repeatedly applies the modulus operation until the remainder is zero.
• LCM Calculation: The lcm function uses the formula involving GCD to compute the LCM.
• Main Function: The main function prompts the user to enter two integers, calculates their LCM, and displays the result.

Output

If you enter 12 and 18, the output will be:

Enter two integers: 12 18
LCM of 12 and 18 is 36

Method 2) C Program to Find LCM of Two Numbers using a Loop

Another straightforward method to find the LCM is by using a loop to iterate through multiples of the larger number until you find one divisible by both numbers.

Code Example

#include <stdio.h>

int lcm_loop(int a, int b) {
    int max = (a > b) ? a : b;

    while (1) {
        if (max % a == 0 && max % b == 0) {
            return max;
        }
        max++;
    }
}

int main() {
    int num1, num2;
    printf("Enter two integers: ");
    scanf("%d %d", &num1, &num2);

    printf("LCM of %d and %d is %d\n", num1, num2, lcm_loop(num1, num2));
    return 0;
}

Explanation of the Code

• Loop for LCM: The lcm_loop function begins with the maximum of the two numbers and increments it by one in each iteration. The loop continues until it finds a number divisible by both input numbers.
• Main Function: The main function prompts the user for input, calculates the LCM using the loop, and prints the result.

Output

If you enter 4 and 5, the output will be:

Enter two integers: 4 5
LCM of 4 and 5 is 20

Method 3) C Program to Find LCM of Two Numbers using Recursion

Recursion is a powerful tool in programming that can simplify complex tasks. Here, we’ll use recursion to find the GCD and subsequently the LCM.

Code Example

#include <stdio.h>

// Recursive function to find GCD
int gcd_recursive(int a, int b) {
    if (b == 0)
        return a;
    return gcd_recursive(b, a % b);
}

// Function to calculate LCM using recursive GCD
int lcm_recursive(int a, int b) {
    return (a * b) / gcd_recursive(a, b);
}

int main() {
    int num1, num2;
    printf("Enter two integers: ");
    scanf("%d %d", &num1, &num2);

    printf("LCM of %d and %d is %d\n", num1, num2, lcm_recursive(num1, num2));
    return 0;
}

Explanation of the Code

• Recursive GCD: The gcd_recursive function calculates the GCD using a recursive approach, which simplifies the logic by calling the function within itself.
• LCM Calculation: The lcm_recursive function uses the recursive GCD to find the LCM.
• Main Function: The main function handles user input and displays the LCM.

Output

If you enter 9 and 6, the output will be:

Enter two integers: 9 6
LCM of 9 and 6 is 18

In this article, we explored three different methods to find the LCM of two numbers in C programming: using the GCD, using a loop, and using recursion. Each method has its strengths, and the choice depends on the specific requirements and constraints of your program. Understanding these approaches provides a solid foundation for tackling a wide range of mathematical problems in C programming.