Matrix operations are fundamental in various fields such as mathematics, computer science, engineering, and more. One of the key operations is the transpose of a matrix, which is widely used in algorithms, data processing, and scientific computing. In this article, we’ll explore how to Write a C program to Find the Transpose of a Matrix, providing three detailed methods with code examples, explanations, and outputs. This guide is tailored for a technical audience with a keen interest in C programming.

Write a C Program to Find the Transpose of a Matrix

What is Matrix Transposition?

Matrix transposition is the process of swapping the rows and columns of a matrix. If you have a matrix A with dimensions m×n, its transpose, denoted as A^T, will have dimensions n×m. The element at the position (i, j) in the original matrix will move to the position (j, i) in the transposed matrix.

For example, given the matrix:

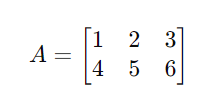
The transpose of matrix A is:

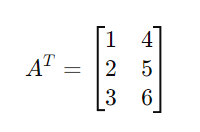
Now, let’s explore how to implement this operation in C.

Method 1) C Program to Find the Transpose of a Matrix using a Temporary Matrix

This is the most straightforward approach to find the transpose of a matrix. Here, we use a temporary matrix to store the transposed values.

Code Example

#include <stdio.h>

void transposeMatrix(int rows, int cols, int matrix[rows][cols], int transposed[cols][rows]) {
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            transposed[j][i] = matrix[i][j];
        }
    }
}

int main() {
    int rows = 2, cols = 3;
    int matrix[2][3] = {
        {1, 2, 3},
        {4, 5, 6}
    };
    int transposed[3][2];

    transposeMatrix(rows, cols, matrix, transposed);

    printf("Transposed Matrix:\n");
    for (int i = 0; i < cols; i++) {
        for (int j = 0; j < rows; j++) {
            printf("%d ", transposed[i][j]);
        }
        printf("\n");
    }
    
    return 0;
}

Explanation of the Code

1. Function Definition: The function transposeMatrix takes the number of rows and columns of the original matrix, the matrix itself, and an empty matrix for storing the transposed values.
2. Nested Loops: The outer loop iterates through each row, while the inner loop iterates through each column. The method swaps the elements, turning the row index into the column index and vice versa.
3. Main Function: The original matrix is defined, and the transposeMatrix function is called.

Output

When you run this program, the output will be:

Transposed Matrix:
1 4 
2 5 
3 6

Method 2) C Program to Find the Transpose of a Matrix using In-Place Transposition for Square Matrices

This method optimizes transposition for square matrices, where the number of rows and columns are equal. It transposes the matrix in-place without requiring additional space.

Code Example

#include <stdio.h>

void transposeSquareMatrix(int size, int matrix[size][size]) {
    for (int i = 0; i < size; i++) {
        for (int j = i + 1; j < size; j++) {
            int temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
}

int main() {
    int size = 3;
    int matrix[3][3] = {
        {1, 2, 3},
        {4, 5, 6},
        {7, 8, 9}
    };

    transposeSquareMatrix(size, matrix);

    printf("Transposed Matrix:\n");
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            printf("%d ", matrix[i][j]);
        }
        printf("\n");
    }
    
    return 0;
}

Explanation of the Code

1. Function Definition: The function transposeSquareMatrix is designed specifically for square matrices.
2. Efficient Transposition: The nested loop starts from the diagonal element (i.e., i + 1), swapping elements above and below the diagonal. This reduces the number of swaps needed and avoids redundant operations.
3. Main Function: The main function initializes a square matrix and calls the transpose function.

Output

The output for this code is:

Transposed Matrix:
1 4 7 
2 5 8 
3 6 9

Method 3) C Program to Find the Transpose of a Matrix using Dynamic Memory Allocation

This method demonstrates how to handle matrix transposition for dynamically allocated matrices, offering greater flexibility for matrices with varying dimensions.

Code Example

#include <stdio.h>
#include <stdlib.h>

void transposeDynamicMatrix(int rows, int cols, int **matrix, int **transposed) {
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            transposed[j][i] = matrix[i][j];
        }
    }
}

int main() {
    int rows = 2, cols = 3;

    int **matrix = (int **)malloc(rows * sizeof(int *));
    for (int i = 0; i < rows; i++) {
        matrix[i] = (int *)malloc(cols * sizeof(int));
    }

    int **transposed = (int **)malloc(cols * sizeof(int *));
    for (int i = 0; i < cols; i++) {
        transposed[i] = (int *)malloc(rows * sizeof(int));
    }

    // Initializing matrix
    int values[2][3] = {
        {1, 2, 3},
        {4, 5, 6}
    };
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            matrix[i][j] = values[i][j];
        }
    }

    transposeDynamicMatrix(rows, cols, matrix, transposed);

    printf("Transposed Matrix:\n");
    for (int i = 0; i < cols; i++) {
        for (int j = 0; j < rows; j++) {
            printf("%d ", transposed[i][j]);
        }
        printf("\n");
    }

    // Freeing allocated memory
    for (int i = 0; i < rows; i++) {
        free(matrix[i]);
    }
    free(matrix);

    for (int i = 0; i < cols; i++) {
        free(transposed[i]);
    }
    free(transposed);

    return 0;
}

Explanation of the Code

1. Dynamic Memory Allocation: malloc is used to allocate memory for both the original and transposed matrices dynamically.
2. Function Definition: The transposeDynamicMatrix function transposes the matrix using dynamic pointers.
3. Memory Management: After transposition, the allocated memory is freed to avoid memory leaks, demonstrating good programming practices.

Output

The output will be:

Transposed Matrix:
1 4 
2 5 
3 6

Matrix transposition is a fundamental operation in C programming, and understanding different methods to perform this task can enhance your coding skills. We explored three approaches:

1. Using a Temporary Matrix: A simple and universal method.
2. In-Place Transposition for Square Matrices: Efficient for square matrices, with no additional memory required.
3. Transpose Using Dynamic Memory Allocation: Offers flexibility for matrices of varying sizes, demonstrating advanced C programming techniques.

Each method has its use case, and selecting the right one depends on the specific requirements of your application. Happy coding!